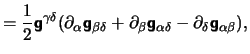The basic quantities and equations of General Relativity
In order to formalize the ideas mentioned in the previous section,
general relativity views
spacetime as a 4-dimensional manifold equipped with a metric
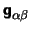 of Lorentzian signature where the Greek indices range from 0 to 3.
At any given point in the manifold the
signature enables one to distinguish between time-like, space-like
and null directions. The metric further induces a whole range of
higher level geometric concepts on the manifold. It defines a
scalar product between vectors which leads to the measurement
of length and the idea of orthogonality. From the metric and
its derivatives one can derive a connection on the manifold which
facilitates the definition of a covariant derivative. The notion
of a derivative is more complicated in a curved manifold than
in the common case of flat geometry and Cartesian coordinates because
the basis vectors will in general vary
from point to point in the manifold. It is therefore no longer possible
to identify the derivative of a tensor with the derivative of its
components. Instead one obtains extra terms involving the derivatives
of the basis vectors. In terms of a covariant derivative these
terms are represented by the connection. In general relativity one
uses a metric-compatible connection defined by
of Lorentzian signature where the Greek indices range from 0 to 3.
At any given point in the manifold the
signature enables one to distinguish between time-like, space-like
and null directions. The metric further induces a whole range of
higher level geometric concepts on the manifold. It defines a
scalar product between vectors which leads to the measurement
of length and the idea of orthogonality. From the metric and
its derivatives one can derive a connection on the manifold which
facilitates the definition of a covariant derivative. The notion
of a derivative is more complicated in a curved manifold than
in the common case of flat geometry and Cartesian coordinates because
the basis vectors will in general vary
from point to point in the manifold. It is therefore no longer possible
to identify the derivative of a tensor with the derivative of its
components. Instead one obtains extra terms involving the derivatives
of the basis vectors. In terms of a covariant derivative these
terms are represented by the connection. In general relativity one
uses a metric-compatible connection defined by
where the Einstein summation convention, according to which
one sums over repeated upper and lower indices, has been used.
These connection coefficients
are also known as the Christoffel symbols and define a covariant
derivative of tensors of arbitrary rank by
where
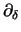 represents the standard partial derivative with
respect to the coordinate
represents the standard partial derivative with
respect to the coordinate
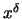 . So for each upper index one adds a term containing the connection
coefficients and for each lower index a corresponding term is subtracted.
With the definition of a covariant derivative we can finally write
down the exact definition of a "straight line" in a curved manifold.
A geodesic is defined as the integral curve of a vector field
. So for each upper index one adds a term containing the connection
coefficients and for each lower index a corresponding term is subtracted.
With the definition of a covariant derivative we can finally write
down the exact definition of a "straight line" in a curved manifold.
A geodesic is defined as the integral curve of a vector field
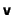 which is parallel transported along itself
which is parallel transported along itself
Based on the covariant derivative we can also give a precise definition
of curvature. For this purpose the Riemann tensor is defined
by
If we use a coordinate basis, i.e.
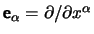 , this definition can be shown to imply that for any vector field
, this definition can be shown to imply that for any vector field
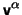
which is commonly interpreted by saying that a vector
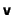 is changed by being
parallel transported around a closed loop unless the curvature vanishes.
In order to describe the effect
of the matter distribution on the geometry of spacetime one defines the
Ricci tensor as the contraction of the Riemann tensor
is changed by being
parallel transported around a closed loop unless the curvature vanishes.
In order to describe the effect
of the matter distribution on the geometry of spacetime one defines the
Ricci tensor as the contraction of the Riemann tensor
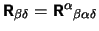 , where again the Einstein summation convention for repeated
indices has been used. The geometry and the matter are then related by
, where again the Einstein summation convention for repeated
indices has been used. The geometry and the matter are then related by
where
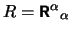 is the Ricci scalar and
is the Ricci scalar and
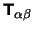 the energy momentum tensor.
The interaction between the matter distribution and the geometry of
spacetime can be summed up in the words of Misner, Thorn and Wheeler:
"Space acts on matter, telling it how to move. In turn, matter
reacts back on space, telling it how to curve".
the energy momentum tensor.
The interaction between the matter distribution and the geometry of
spacetime can be summed up in the words of Misner, Thorn and Wheeler:
"Space acts on matter, telling it how to move. In turn, matter
reacts back on space, telling it how to curve".