I recently came across a very funny math thing, which has to do with the volume of spheres in N dimensions. Sure, not really meaningful from a physical point of view, but still very funny to think about it.
I led a discussion on this during one of the 2018 TAPIR Postdoc lunches at Caltech. Thanks to everybody that was there!
Here is the thing: The volume of an N-dimensional sphere goes to zero (!) as the number of dimensions increases. In other terms, balls are empty in very high dimensional spaces. That’s sooo weird.
To be more precise, one should really say that the ratio between the volume of a sphere and that of a cube goes to zero. Imagine putting a circle inside a square in 2D: the area of the square is \(4r^2\), while the area of the circle is \(\pi r^2\). What’s left (“the corners”) have area \((4-\pi) r^2\). In 2D, there’s more area in the circle than in the corners. It turns out that if you crank up the number of dimensions, all of the volume is contained in the corners!
Of course, I couldn’t believe this and had to convince myself with both maths and “experiments”.
Maths…
So, let’s calculate the volume of a sphere in N dimensions. There are many ways to carry out this proof; this is a simple one taken from the source of all knowledge. We expect the volume to scale with the radius as \(V_N(r)\propto r^N\). We want to find the constant of proportionality as a function of N.
We deal with numbers \(\boldsymbol{x}=\{{x_1, x_2,…, x_n}\}\in \mathbb{R}^n\), which are really arrays of reals. We need a function and, for simplicity, let’s just take a Gaussian
\(f(\boldsymbol{x}) = \exp\left( – \frac{1}{2} \sum_{i=1}^N x_i^2 \right) = \prod_{i=1}^N \exp\left( – \frac{1}{2} x_i^2 \right)\)The idea is to integrate this function in two different sets of coordinates and compare the result. First, let’s integrate in cartesian coordinates:
\(\int_{\mathbb{R}^n} f(\boldsymbol{x}) d \boldsymbol{x} = \int_{-\infty}^{+\infty}…\int_{-\infty}^{+\infty} f(\boldsymbol{x}) dx_1… dx_N = \prod_{i=1}^N \int_{-\infty}^{+\infty}\exp\left( – \frac{1}{2} x_i^2 \right) dx_i = (2\pi)^{N/2}\)Each of those piece is a single-dimensional gaussian, and we know that a gaussians integrate to \(\sqrt{2\pi}\). We have N of them, so that gives you \((2\pi)^{N/2}\).
Now, let’s do the same thing in spherical coordinate. The distance from the origin is \(r^2=\sum_i x_i^2\). We divide \({\mathbb{R}^n}\) into shells of dimension N-1 and then integrate radially, i.e.
\(\int_{\mathbb{R}^n} f(\boldsymbol{x}) d \boldsymbol{x} = \int_0^\infty \int_{S_{N-1}(r)} \exp\left(-\frac{1}{2} r^2\right) dA dr = \int_0^\infty \exp\left(-\frac{1}{2} r^2\right) \left[\int_{S_{N-1}(r)} dA\right] dr\)
The term in brakets is the surface of a N-1 dimensional sphere, which is expected to scale as \(r^{N-1}\), i.e.
\(\int_{S_{N-1}(r)} dA = A_{N-1}(r) = A_{N-1}(1) r^{N-1}\)So, the integral above becomes (substitute \(t=r^2/2\))
\(… = A_{N-1}(1) \int_0^\infty r^{N-1} \exp\left(-\frac{1}{2} r^2\right) = A_{N-1}(1) 2^{(n-2)/2}\int_0^\infty e^{-t} t^{(n-2)/2} dt = A_{N-1}(1) 2^{(n-2)/2} \Gamma\left(\frac{n}{2}\right)\)The last thing is a Gamma function, which is defined by the integral above, so not much to say there. It basically the generalization of factorials to non-integer numbers.
Now we can equate the integrals \(\int_{\mathbb{R}^n} f(\boldsymbol{x}) d \boldsymbol{x}\) computed with both sets of coordinates to obtain
\(A_{N-1}(1) = \frac{2 \pi^{n/2}}{\Gamma\left(\frac{n}{2}\right)}\)We thus have the surface area of the (N-1)dimensional sphere
\(A_{N-1}(r) = \frac{2 \pi^{n/2}}{\Gamma\left(\frac{n}{2}\right) } r^{N-1}\)The N-volume is now obtained by integrating the surface \(A_{N-1}(r)\) along \(r\) (easy! it’s a polinomial!)
\(V_N(r) = \int_0^\infty A_{N-1}(r) dr = \frac{2 \pi^{n/2}}{n \Gamma\left(\frac{n}{2}\right)}r^N = \frac{\pi^{n/2}}{\Gamma\left(\frac{n}{2}+1\right)}r^N\)where at the end we used the Gamma function property \(z\Gamma(z) = \Gamma(z+1)\).
So, this is the final result:
\(V_N(r) = \frac{\pi^{n/2}}{\Gamma\left(\frac{n}{2}+1\right)}r^N\)The N-dimensional volume scale as the inverse of a Gamma function. So, it goes to zero, and it goes to zero really fast! Faster than an exponential, actually. This is because \(\Gamma(z+1)\sim \sqrt{2 \pi z}(z/e)^z\) as \(z\to\infty\) (this thing is called Stirling formula).
Code…
That’s hard to believe, so I had to do an experiment, which for me really means putting this thing into a computer. Here is the simple python code I wrote to compute the N-dimensional volume.
It’s a Monte-Carlo strategy, and it’s actually very simple. We throw a large number of random points in the N-dimensional cube and select those that are inside the sphere. The volume of the sphere is the volume of the cube times the fraction of accepted points
\(V_{\rm N sphere} = V_{\rm N cube} \frac{N_{\rm accepted}}{N_{\rm total}}\).We do this for many dimensions D up to 30 and check the volumes we find against the exact solution we proved above. If you run that code, this is what you get:
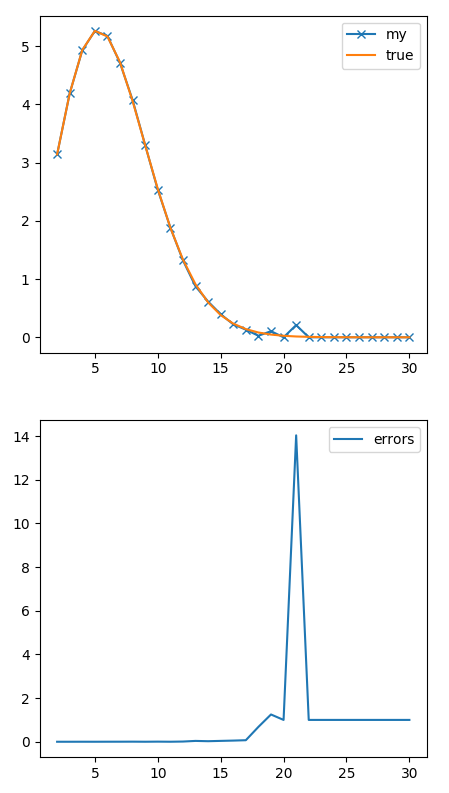
D=2 N=10000000 N_in=7854391 V=3.14176 Sol=3.14159 diff=0.00005 t=0.63s D=3 N=10000000 N_in=5236198 V=4.18896 Sol=4.18879 diff=0.00004 t=0.92s D=4 N=10000000 N_in=3084039 V=4.93446 Sol=4.93480 diff=0.00007 t=1.16s D=5 N=10000000 N_in=1645407 V=5.26530 Sol=5.26379 diff=0.00029 t=1.35s D=6 N=10000000 N_in=808056 V=5.17156 Sol=5.16771 diff=0.00074 t=1.74s D=7 N=10000000 N_in=370005 V=4.73606 Sol=4.72477 diff=0.00239 t=1.89s D=8 N=10000000 N_in=158915 V=4.06822 Sol=4.05871 diff=0.00234 t=2.08s D=9 N=10000000 N_in=064144 V=3.28417 Sol=3.29851 diff=0.00435 t=2.50s D=10 N=10000000 N_in=025101 V=2.57034 Sol=2.55016 diff=0.00791 t=3.78s D=11 N=10000000 N_in=009097 V=1.86307 Sol=1.88410 diff=0.01117 t=3.54s D=12 N=10000000 N_in=003223 V=1.32014 Sol=1.33526 diff=0.01133 t=3.11s D=13 N=10000000 N_in=001055 V=0.86426 Sol=0.91063 diff=0.05092 t=3.27s D=14 N=10000000 N_in=000382 V=0.62587 Sol=0.59926 diff=0.04439 t=3.41s D=15 N=10000000 N_in=000114 V=0.37356 Sol=0.38144 diff=0.02068 t=3.62s D=16 N=10000000 N_in=000026 V=0.17039 Sol=0.23533 diff=0.27594 t=3.65s D=17 N=10000000 N_in=000012 V=0.15729 Sol=0.14098 diff=0.11566 t=3.80s D=18 N=10000000 N_in=000002 V=0.05243 Sol=0.08215 diff=0.36176 t=4.06s D=19 N=10000000 N_in=000001 V=0.05243 Sol=0.04662 diff=0.12456 t=4.54s D=20 N=10000000 N_in=000001 V=0.10486 Sol=0.02581 diff=3.06316 t=4.47s D=21 N=10000000 N_in=000000 V=0.00000 Sol=0.01395 diff=1.00000 t=5.10s D=22 N=10000000 N_in=000000 V=0.00000 Sol=0.00737 diff=1.00000 t=5.42s D=23 N=10000000 N_in=000000 V=0.00000 Sol=0.00381 diff=1.00000 t=5.27s D=24 N=10000000 N_in=000000 V=0.00000 Sol=0.00193 diff=1.00000 t=5.68s D=25 N=10000000 N_in=000000 V=0.00000 Sol=0.00096 diff=1.00000 t=6.46s D=26 N=10000000 N_in=000000 V=0.00000 Sol=0.00047 diff=1.00000 t=6.16s D=27 N=10000000 N_in=000000 V=0.00000 Sol=0.00022 diff=1.00000 t=6.51s D=28 N=10000000 N_in=000000 V=0.00000 Sol=0.00010 diff=1.00000 t=6.99s D=29 N=10000000 N_in=000000 V=0.00000 Sol=0.00005 diff=1.00000 t=6.91s D=30 N=10000000 N_in=000000 V=0.00000 Sol=0.00002 diff=1.00000 t=7.29s
For D=2 we get 3.14… which is \(\pi\). The volume then goes up till D=5. That’s the number of dimensions in which a sphere is “maximally filling”. After that, it decreases like crazy. This code is really good up only up to D=15 or so. After that, the sphere is so small that the number of points \(N_{\rm accepted}\) is basically zero and the error made on the predictions is close to 100%. This is the same information in a plot. The two solutions seem to agree on that scale, but if you look at the errors (bottom plot), that becomes huge.
BTW, I still think it’s weird. What happens if you pour water in an N-dimensional spherical ball? Can’t fit any water in it. Wait. What’s N-dimensional water?
